Class 11 Physics CBSE Chapter 3 (One Dimensional Motion) Important Question and Answer

 Question 1.

Prove that the average velocity of a particle over an interval of time is either smaller than or equal to the average speed of the particle over the same interval.
Answer:
Average velocity is defined as the ratio of the total displacement to the total time. Average speed is defined as the ratio of the total distance to the total time. Since displacement is less than or equal to the distance, therefore the average velocity is less than or equal to the average speed.

Question 2.
Two trains each of the length 109 m and 91 m are moving in opposite directions with velocities 34 km h-1 and 38 km h-1 respectively. At what time the two trains will completely cross each other?
Answer:
Let l1, l2 be the lengths of the two trains.
v1, v2 be their velocities respectively.

∴ l1 = 109m, l2 = 91 m, v1 = 34kmh-1, v2 = 38kmh-1.
As the trains are moving in opposite directions so relative velocity of the trains is given by
v1 – (- v2) = v1 + v2
= 34 + 38 = 72 kmh-1
= 72 × 518 = 20 ms-1

Total distance to be covered by the two trains in crossing each other
= l1 + l2= 109 + 91 = 200 m

If t be the time taken in crossing, then t can be calculated using the relation
x = vt
or
t = 20020 = 10s

Question 3.
Ambala is at a distance of 200 km from Delhi. Ram sets out from Ambala at a speed of 60 km h-1 and Sham set out at the same time from Delhi at a speed of 40 km h-1. When will they meet?
Answer:
S = 200 km. Let VR and vs be the speeds of Ram and Sham respectively moving in opposite directions.
∴ vR = 60 kmh-1, vS = 40 kmh-1.

∴ Relative velocity of Ram w.r.t. Sham is
VRS = VR – (- VS)
= VR + VS
= 60 + 40 = 100 kmh-1

If t = time after which they will meet, then
t = time taken in covering 200 km distance with VRS
i.e. t = 200vRS=200 km100kmh−1 = 2h.

∴ Time after which they meet = 2h.

Question 4.
A car travelling at a speed of 60 km h-1 on a straight road is ahead of a scooter travelling at a speed of 40 km h-1. How would the relative velocity be altered if the scooter is ahead of the car?
Answer:
vc = speed of car = 60 kmh-1
vs = speed of scooter = 40 kmh-1
vcs = relative velocity of car w.r.t. scooter
= vc – vs
= 60 – 40
= 20 kmh-1.           

 Similarly vsc = relative velocity of scooter w.r.t. car

= vs – vc
= 40 – 60
= – 20 kmh--1

   Thus we conclude that the magnitude of the relative velocity is the same in both cases but the direction of relative velocity is reversed if the scooter is ahead of the car.

Question 5.
Draw the position-time graphs for two objects initially occupying different positions but having zero relative velocity.
Answer:
The positive T time graphs for two objects initially occupying different positions but having zero relative velocity are parallel to each other as shown in Fig.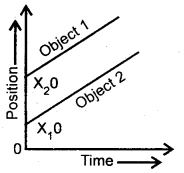

Question 6.
A ball is thrown vertically upward with a velocity of 20 ms-1. It takes 4 seconds to return to its original position. Draw a velocity-time graph for the motion of the ball and answer the following questions:
At which point P, Q, R, the stone has :
(a) reached its maximum height.
(b) stopped moving?
Answer:
Let P represent the initial position at the time when the ball is thrown vertically upward.
Q represents the highest point reached by the ball.
R represents the original position of the ball after 4 seconds.

Thus the velocity-time graph for the motion of the ball is as shown in Fig.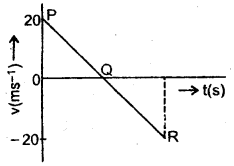

(a) We know that at the highest point, the velocity of the object is zero. So stone will reach its maximum height corresponding to point Q.

(b) The stone has stopped moving at point Q because at Q, v = 0.

Question 7.
“It is the velocity and not the acceleration which decides the direction of motion of a body.” Justify this statement with the help of a suitable example.
Answer:
The direction of velocity is always in the direction of motion of the body whereas the direction of acceleration may or may not be in the direction of motion of the body. Thus we conclude that it is the velocity that decides the direction of motion of the body.

Example: When a ball is thrown vertically upwards, the direction of motion of the ball and velocity is the same i.e. vertically upwards. On the other hand, the acceleration due to gravity on the ball acts vertically downwards i.e. opposite to the direction of motion of the ball.

Question 8.
Two buses A and B starting from the same point move in a mutually perpendicular direction with speeds uA km h-1 and uB km h-1 respectively. Calculate the relative velocity of A w.r.t B.
Answer:
Since uA and uB are in mutually perpendicular directions, they will cover uA and uB km in one hour respectively. Thus if v km be the separation between them in one hour,
Then v = 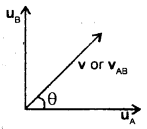u2A+u2B−−−−−−−√

Thus if vAB be the relative speed of A w.r.t. B, then
vAB = u2A+u2B−−−−−−−√ kmh …(1)

If θ be the direction of vAB w.r.t. uA, Then
tan θ = uAvAB=uAu2A+u2B√ …(2)

Thus, equations (1) and (2) give the magnitude and direction of relative velocity of A w.r.t. B.

Question 9.
A draw velocity-time graph for a body which
(i) accelerates uniformly from rest,
Answer:
The required velocity-time graph is shown in Fig. here

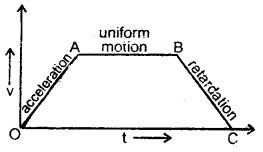
OA part of the graph represents the uniformly accelerated motion of the body.

(ii) then moves with a uniform velocity and
Answer:
AB part of the graph represents motion with uniform velocity.

(iii) finally retarded uniformly.
Answer:
BC part of the graph represents motion with uniform retardation of the body.

Question 10.
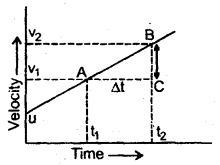
From a velocity-time graph, how do you calculate the average acceleration of a moving body?
Answer:
The slope of the velocity-time curve gives the acceleration of the body. For this purpose, we take a small interval of time Δt and a corresponding change in velocity Δv such that Δt = t2 – t1 and Δv = v2 – v1. Over a very small interval of time Δt, arc AB may be considered as a chord AB, then.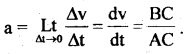

Question 11.
State whether the following two graphs in Fig. here represent the same type of motion or not. Name the motion of the particle.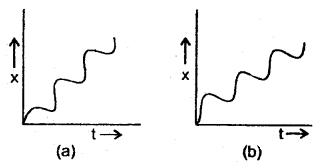

Answer:

Yes. Both of these graphs represent the same type of motion. The motion of the particle represented by these graphs is non-uniform motion i.e. the particle is moving with variable velocity.

Question 12.
Draw the velocity-time graph for an object moving with uniform velocity. What does it show for t < 0?
Answer:
As the object moves with uniform velocity, the magnitude and direction of its velocity remain the same at all points of its path. Thus v – t graph’ is a straight line parallel to the time axis as shown in Fig. here.

For t < 0, the v – t graph shows that the object is at rest till t = 0.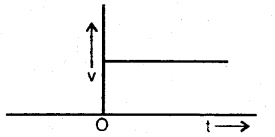

Question 13.
The displacement time graph of a body is shown in the figure below. What does the curve for t < 0 and t > 0 show?
Answer:
The line ∥ to t – axis in fig. shows that the object is at rest t ∥ t = 0. For t > 0, it shows that it is still at rest but at some another poi it at a distance XQ from the point for t < 0.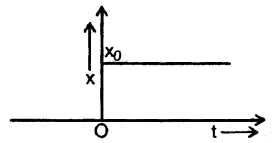

Question 14.
Distinguish between one, two and three-dimensional motion.
Answer:
The motion of an object along a straight line in a fixed direction is called one-dimensional motion.

• The motion of an object in a plane is called two-dimensional motion
• The motion of an object in space is called three-dimensional motion

Question 15.
A ball thrown upward reaches a height and comes bad downward. Out of the following statements, which one is true for displacement, velocity and acceleration.
(a) It varies continuously but never changes the sign.
(b) It varies continuously with the maximum, in the beginning, being zero at the top.
(c) It remains constant throughout the course of the journey.
(d) It only changes the sign when the ball is at the top.
Answer:

• Statement (a) is true for displacement as it varies from starting
• Statement (b) is true for velocity as it is maximum at the time o projecting the ball and becomes zero at the highest point i.e. top.
• Statement (c) is true for acceleration as it is always constant throughout the course of the journey and is equal to ‘g’.

Question 16.
Derive the expression for the time taken by a body dropped from a height h to reach at Earth.
Answer:
Here,
initial velocity, u = 0
acceleration, a = g
distance covered, S = h

Let t = time taken
Using the relation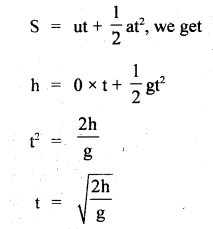

Question 17.
In which of the following cases, the body may be considered a point object:
(a) A railway carriage moving without jerks between two stations.
(b) A monkey sitting on the shoulder of a cyclist moving smoothly in a circular track.
1 A beaker tumbling down the edge of a table, A spinning cricket ball that turns sharply on hitting the ground.
Answer:
(a) and (b) as the distance moved by the bodies is much larger; the size of the body.

Question 18.
What do you understand by positive and negative time?
Answer:
The origin of time is called zero time. The instant of time which is after the origin of time is called positive time and the instant of, which is taken before the origin of time is called negative time.

Question 19.
If the displacement time graph of a particle is parallel to the displacement axis (b) the time axis, what will be the velocity particle? Why?
Answer:
(a) When the displacement-time graph is parallel to the displacement axis, the velocity of the particle is infinity.
We know that velocity = ΔxΔt
when the graph is parallel to the displacement axis, then Δt = 0, so velocity = infinity.

(b) When the displacement-time graph is parallel to the time axis, the velocity of the particle is zero as in this case Δx = 0.

Question 20.
An object is in uniform motion along a straight line. What will be its position-time graph if
(a) x0 = +ve, v = +ve,
(b) x0 = +ve, v = – ve,
(c) x0 = – ve, v = +ve,
(d) x0 = – ve, v = – ve.
The letters x0 and v represent the position of the object at time t = 0 and the uniform velocity of the object respectively.
Answer:
The position of an object at any time t moving with a uniform velocity along a straight line is given by
x = x0 + vt ….(1)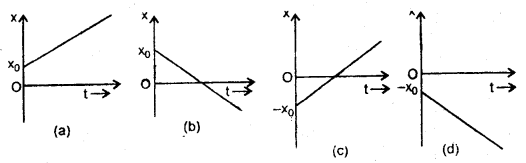

(a) If X0 > 0, v > 0 i.e. both positive, then the position-time graph is as shown in Fig. (a).
(b) If X0 = +ve, v = – ve, then the x – t graph is as shown in Fig. (b).
(c) If X0 = – ve, v = +ve, then the x – t graph is as shown in Fig. (c).
(d) If both x0 and v are – ve, then the x -t graph is as shown in Fig. (d).

Question 21.
Define displacement. What are its characteristics?
Answer:
It is defined as the change in the position of an object in a particular direction.

Characteristics of displacement:

1. It is a vector quantity.
2. It has units of length.
3. The magnitude of displacement is called distance.
4. The diode valve curve between voltage and current is quite like curve ABCD.

Question 22.
A stone is dropped from the top of a tower and after one second, another stone is dropped from a point 20 m below the top. If both the stones reach the ground at the same time, calculate the height of the tower (take g = 10 mf2).

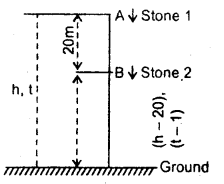
Answer:
The given situation is shown in fig.
Let t = time taken by the first stone to reach the ground
h = height of the tower
u1 = initial velocity O
∴ using equation

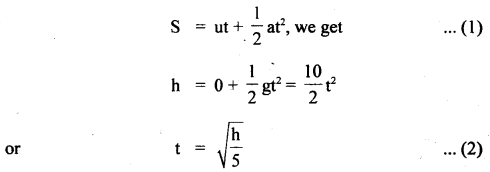
∴ t – 1 = Time taken by the second stone to reach the ground and
h – 20 = height of the point from where it is dropped l.
∴ u2 = initial velocity = 0

Thus using equation (1), we get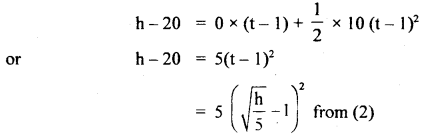

Question 23.
A body travels half of its total path in the last second of its fall from rest. Calculate the time and height of fall.
Answer:
Let h = height of fall
t = time of fall
a = g = 9.8ms-2
u = 0

using equation,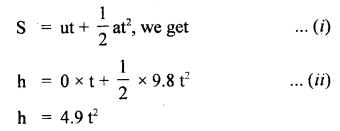

Also according to the statement first half i.e. h2 is covered in (t – 1)s.
∴ using (i), we get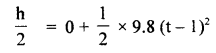


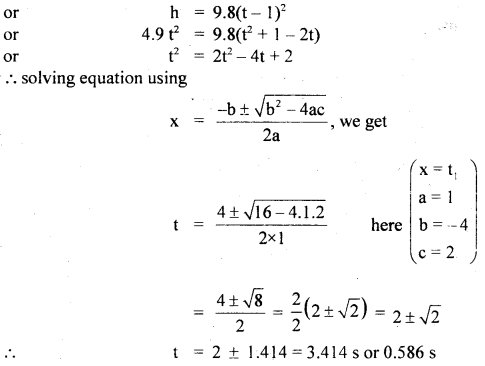
As last half of the journey takes 1 s, so t cannot be less than 1 s.

∴ t = 3.41s
∴ From(ii), h = 4.9 × (3.414)2
= 57.11 m
∴ h = 57.11, t = 3.414s.

Question 24.
A train moves from one station to another in 2h time. Its speed during the motion is shown in fig. Calculate
(a) the maximum acceleration during the journey.
(b) the distance covered during 0.75 to 1.00 h interval.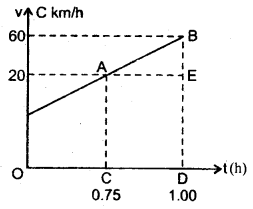

Answer:
(a) Maximum acceleration during the journey
= slope of AB part of the graph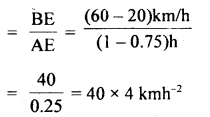

∴ acceleration = 160 kmh-2.

(b) Distance covered during the interval 0.75 to 1.00 h
= Area under the v -1 curve from 0.75 to 1.00
= Area of trapezium CABD
= Area of rectangle AEDC + area of AAEB

Question 25.
When the speed of the car is y, the minimum distance over which it can be stopped is z. If the speed of the car becomes v, then what will be the minimum distance over which it can be stopped?
Answer:
Case I:
Here, the initial velocity of car = v
The final velocity of car = 0

Let a = acceleration of car Distances covered before stopping = x
∴ Using the equation,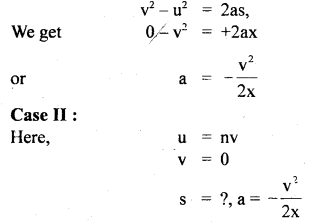

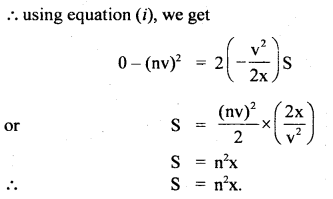
Question 26.
A body describes 10m in the third second and 12m in the Sth second with uniform acceleration. Find the distance covered by it in :
(a) next 3′ seconds and
(b) 8th second of its motion.
Answer:
Let the initial velocity of body = v
and let acceleration of body = a
Also, we know that distance covered during the nth second is given by
Snth =u + a2(2n – 1)

Distance travelled in 3rd and 5th second is: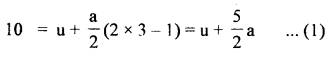


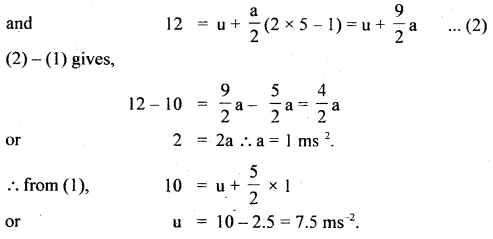
(a) using the equation, S = ut + at2, Let us find the distance covered by the body in 5s and 8 seconds.
Take u = 7.5,ms-1, a= I ms2

If x1 and x2 be the distances covered in 5s and 8s respectively.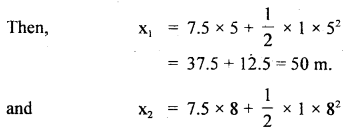

= 60 + 32 = 92 m

∴ Distance travelled by the body in next 3 seconds is given by
= x2 – x1
= 92 – 50 = 32 m

(b) The distance trave1ìdby the body in 8th second (x8) is given by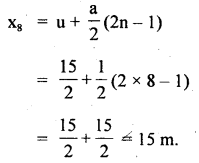

Question 27.
The velocity of an object (ms-1) moving along a straight line is given by
v = 10 + 3t2 …. (1)
Find (a) change in velocity in the interval when t = 2s and 5s.
(b) average acceleration in the same interval.
(c) instantaneous acceleration at t = 4s.

Answer:
Comparing equation (1), with the equation v = u + at, we find that u = 10ms-1,
(a) Now velocity of the object after 2 and 5 seconds is calculated as :
v = 10 + 3t2
putting t = 2, v = 10 + 3 × 22 = 10 + 3 × 4 = 22ms-1
putting t = 5, v = 10 + 3 × 52 = 10 + 3 × 25 = 85 ms-1.
∴ Change in velocity from 2s to 5 s
= 85 – 22 = 63 ms-1.

(b) We know that average acceleration in a given time interval is given by
aav = ΔvΔt

Thus aav in the interval 2s to 5 is given by
aav = 85−225−2=633 = 21 ms-2.

(c) We know that instantaneous acceleration is given by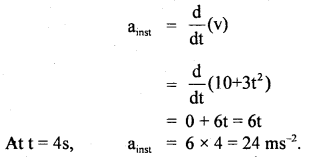

Question 28.
A car travels at a rate of 30 km h-1 for 5 minutes and then at 40 km h-1 for 10 minutes.
Find (i) the total distance covered by the car
(ii) the average speed of the car.
Answer:
v1 = 30 kmh-1 t1 = 5 min = 560 h = 112 h.
If S1 be the distance covered in 5 min., then
S1 = v1 t1 = 30 × 112 = 52 km = 2.5 km

Now v2 = 40 kmh-1, t2 = 10 minutes = 16 h

If S2 = distance covered in 10 min., then
S2 = v2 t2 = 40 × 16 = 203 km = 6.67 km.

(i) If S be the total distance, then
S = S1 + S2 = 2.5+ 6.67 = 9.17 km.

(ii) If vav be the average speed of the car,