Question 1.
What is the source of the kinetic energy of the falling raindrops?
Answer:
It is the gravitational potential energy that is converted into kinetic energy.
Question 2.
A spring is stretched. Is the work done by the stretching force positive or negative?
Answer:
Positive because the force and the displacement are in the same direction.
Question 3.
What is the type of collision when?
(a) Does a negatively charged body collide with a positively charged body?
Answer:
Perfectlyjnelastic collision.
(b) Do macroscopic bodies collide?
Answer:
Inelastic collision.
(c) Do two quartz balls collide?
Answer:
Perfectly elastic collision.
Question 4.
(a) Give two examples of potential energy other than gravitational potential energy.
Answer:
Electrostatic P.E. and elastic P.E.
(b) Give an example of a device that converts chemical energy into electrical energy.
Answer:
Daniell cell.
(c) Heat energy is converted into which type of energy in a steam engine?
Answer:
Mechanical energy.
(d) Where is the speed of the swinging pendulum maximum?
Answer:
At the bottom of the swing.
(e) A heavy stone is lowered to the ground. Is the work done by the applied force positive or negative?
Answer:
Negative work.
Question 5.
What is the work done by the centripetal force? Why?
Answer:
Zero. This is because the centripetal is always perpendicular to the displacement.
Question 6.
(a) What is the work done by the tension in the string of simple pendulum?
Answer:
zero
(b) What is the work done by a porter against the force of gravity when he is carrying a load on his hand and walking on a horizontal platform?
Answer:
zero
(c) Name the force against which the porter in part (A) is doing some work.
Answer:
Frictional force.
Question 7.
When an arrow is shot, wherefrom the arrow will acquire its K.E.?
Answer:
It is the potential energy of the bent bow which is converted into K.E.
Question 8.
When is the exchange of energy maximum during an elastic collision?
Answer:
When two colliding bodies are of the same mass, there will be a maximum exchange of energy.
Question 9.
Does the work done in raising a load onto a platform depend upon how fast it is raised?
Answer:
The work done is independent of time.
Question 10.
Name the parameter which is a measure of the degree of elasticity of a body.
Answer:
Coefficient of restitution.
Question 11.
When a ball is thrown up, the magnitude of its momentum first decreases and then increases. Does this violate the conservation of momentum principle?
Answer:
No. This is because the momentum of the system (ball and air molecules) remains constant. When the momentum of the ball decreases, the momentum of air molecules in contact increases and vice-versa.
Question 12.
In a tug of war, one team is slowly giving way to the other. What work is being done and by whom?
Answer:
+ve. The winning team is performing work over the losing team.
Question 13.
A light and a heavy body have equal momentum. Which one of them has more K.E.?
Answer:
The lighter body has more K.E.
Question 14.
By using simple mechanical devices such as a lever, wedge, inclined plane, pulley, wheel, etc. we can do work even by applying small force. What makes it possible to do so?
Answer:
These mechanical devices multiply forces.
Question 15.
Two protons are brought closer. What is the effect on the potential energy of the system?
Answer:
Work is done to overcome the force of repulsion, so the potential energy of the system increases.
Question 16.
Where is the energy of a vertically projected body maximum?
Answer:
It is the same at all points. This is in accordance with the law of conservation of energy.
Question 17.
Out of a pair of identical springs of force constants, 240Nm-1 one is compressed by 10 cm and the other is stretched by 10 cm. What is the difference in the potential energies stored in the two springs?
Answer:
The difference in potential energies is zero. This is because
Ep =
Question 18.
What should be the angle between the force and the displacement for maximum and minimum work?
Answer:
For maximum work, θ = 0° and for minimum work θ = 90°.
Question 19.
Does the P.E. of a spring decreases/increase when it is compressed or stretched? Why?
Answer:
P.E. of a spring increases in both cases. This is because work is done by us in compression as well as in stretching the spring.
Question 20.
Can a body have momentum without energy?
Answer:
No, because for momentum, it must have some velocity and hence energy.
Question 21.
What type of energy is stored in the spring of the watch?
Answer:
Potential energy.
Question 22.
Can a body have energy without momentum?
Answer:
Yes, everybody has some internal energy due to the thermal agitation of the particles of the body. But the vector sum of linear momenta of the moving particles may be zero. It may have energy due to its position (P.E.) and thus momentum is zero.
Question 23.
In which motion, momentum changes but not the K.E.?
Answer:
In uniform circular motion.
Question 24.
Is the whole of K.E. lost in any perfectly inelastic collision?
Answer:
No, only as much K.E. is lost as is necessary for the conservation of linear momentum.
Question 25.
Can the P.E. of an object be negative?
Answer:
Yes, it can be negative when the forces involved are attractive.
Question 26.
The momentum of a body is increased by 50%. What is the percentage change in its K.E.?
Answer:
When the momentum is increased by 50%, velocity increases by
i.e. velocity becomes
i.e.
Question 27.
What is the work done by Earth’s gravitational force in keeping the moon in its orbit in a complete revolution?
Answer:
Zero, because gravitational force is a conservative force.
Question 28.
A spring is cut into two equal halves. How is the spring constant of each half affected?
Answer:
The Spring constant of each half becomes twice the spring constant of the original spring.
Question 29.
What happens to the energy of our watch which we wind once a day?
Answer:
The work done in winding the watch is stored as P.E. in the spring which is converted into K.E. of the moving parts of the watch.
Question 30.
Is collision possible even without actual contact of the colliding particles? Give example.
Answer:
Yes, such collision is called collision at a distance. The collision between subatomic particles (like proton and neutrons) are examples of such collisions.
Question 31.
An airplane’s velocity is doubled,
(a) What happens to its momentum? Is the law of conservation of momentum obeyed?
Answer:
The momentum of the airplane will be doubled. Yes, the law of conservation of momentum will also be obeyed
because the increase in momentum of the airplane is simultaneously accompanied by an increase in momentum of exhaust gases.
(b) What happens to its kinetic energy? Is the law of conservation of energy obeyed?
Answer:
K.E. becomes four times. Yes, the law of conservation of energy is obeyed with the increase in K.E. coming from the chemical energy of fuel i. e. from the burning of its fuel.
Question 32.
In a thermal station, coal is used for the generation of electricity. Mention how energy changes from one form to the other. before it is transformed into electrical energy?
Answer:
When coal is burnt, heat energy is produced which converts water into steam. This steam rotates the turbine and thus heat energy is converted into mechanical energy of rotation. The generator converts this mechanical energy into electrical energy.
Question 33.
Chemical, gravitational and nuclear energies are nothing but potential energies for different types of forces in nature. Explain this statement clearly with examples.
Answer:
A system of particles has potential energy when these particles are held a certain distance apart against some force. For example, chemical energy is due to the chemical bonding between the atoms. Gravitational energy arises when the objects are held at some distance against the gravitational attraction.
Nuclear energy arises due to the nuclear force acting between the nuclear particles.
Question 34.
A man can jump higher on the moon than on Earth. With the same effort can a runner improve his timing for a 100 m race on the moon as compared to that on Earth?
Answer:
Man can jump higher on the moon because the acceleration due to gravity on the moon is less than that on the Earth. But acceleration due to gravity does not affect the horizontal motion. Hence the runner can’t improve his timing on the moon for the 100 m race.
Question 35.
How many MeV are there in a 1-watt hour?
Answer:
We know that 1 watt hour = 1 JS-1 × 3600 s = 3600 J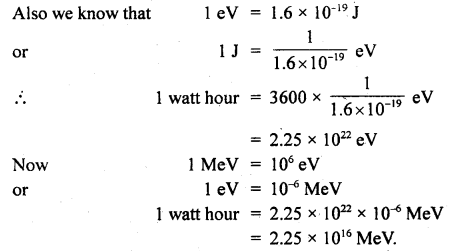
Question 36.
Two bodies A and B having masses mA and mB respectively have equal K.E. If pA and pB be their respective momenta, then prove that the ratio of momenta is equal to the square root of the ratio of respective masses. fc.
Answer:
Let vA and vB be the velocities of A and B respectively.
Since their kinetic energies are equal,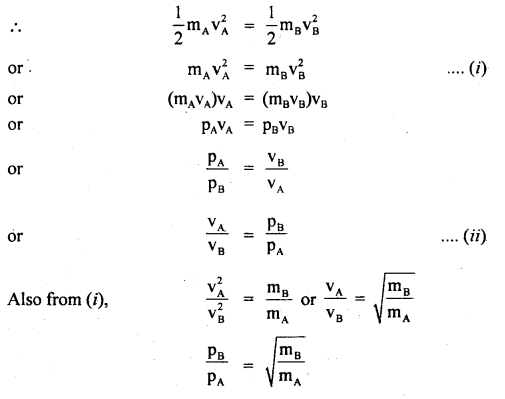

Hence Proved
Question 37.
An engine draws a train up an incline of 1 in 100 at the rate of 36 km h-1. If the resistance due to friction is 5 kg wt per ton, calculate the power of the engine. Mass of train and engine is 100
Answer:
Here, m = 100 metric ton = 100 × 1000 kg
Total force of friction,
f1 = 100 × 5 = 500 kg wt
= 500 × 9.8 N = 4900 N
sin θ =
Let f2 = Downward force on the train
= component of its weight acting in downward direction parallel to the inclined plane = mg sin θ
= 100 × 1000 × 9.8 ×
If F be the total force against which engine has to work, then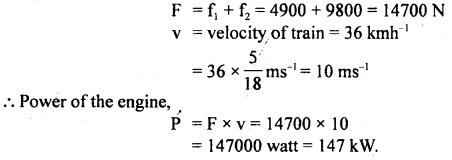
Question 38.
Calculate the work done and power of an engine that can maintain a speed of SO ms-1 for a train of mass 3 × 106 kg on a rough level track for 5 km. The coefficient of friction is 0.05. Given g = 10 ms-2.
Answer:
Here,
Question 39.
A 10 kg block slides without acceleration down a rough inclined plane making an angle of 20° with the horizontal. Calculate the work done over a distance of 1.2 m when the inclination of the plane is increased to 30°.
Answer:
Here, angle of sliding = 20°
μ = coefficient of friction
= tan 20° = 0.3647
S = 1.2 m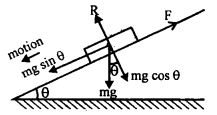
m = mass of block = 10 kg.
Let a = acceleration when the inclination is increased to 30° and F be the value of limiting friction then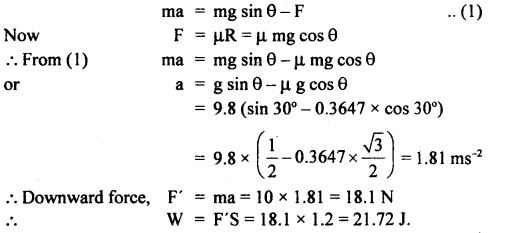
Question 40.
A bullet of mass 0.03 kg moving with a speed of 400 ms-1 penetrates 12 cms into a fixed block of wood. Calculate the average force exerted by the wood on the bullet.
Answer:
Here,
mass of bullet, m = 0.03 kg
initial K.E. =
Final K.E. =
∴ ΔK = Loss in kinetic energy = 2400 J
Let F = average force applied by block on bullet
S = 0.12 m
∴According to work energy principle
W = ΔK
or
FS = ΔK
or
F × 0.12 = 2400
or
F = 2 × 104 N
Question 41.
A boy of mass 50 kg sits in a swing suspended, by a rope 5 m long. A person pulls the swing to one side so that the rope makes an angle of 30° with the vertical. What is the gain in gravitational P.E. of the boy?
Answer:
Here, θ = 30°
OA = OB = 5 m …. (i)
m = 50 kg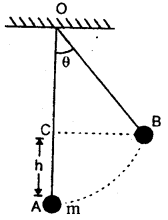
Vertical height through which boy at B rises up is given by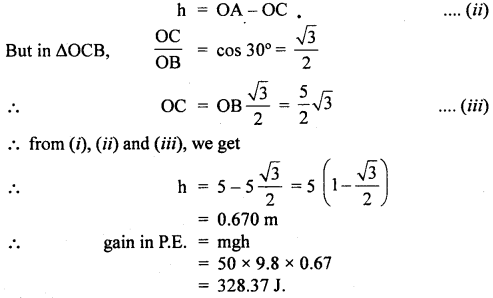
Question 42.
(a) bullet of mass 20 g moving with a velocity of 500 ms-1 strikes a tree and goes out from the other end. with a velocity of 400 ms-1. Calculate the work done in passing through the tree.
Answer:
Here m = 0.02 kg
u = 500 ms-1
v = 400 ms-1
w = ?
from work energy theorem, work done loss in K.E.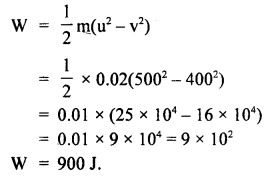
(b) A bullet of mass 0.01 kg is fired horizontally into a 4 kg wooden block at rest on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet remains embedded in the block and the combination moves 20 m before coming to rest. With what speed did the bullet strike the block?
Answer:
Here S = 20 m
μ = 0.25
M = mass of block = 4 kg
m = mass of bullet = 0.01 kg
∴ R = normal reaction = Mg = 4 × 9.8
F = μR = 0.25 × 4 × 9.8 = 9.8 N
v = 0
u = ?
or
loss in KE. = work done by the force of friction against the block.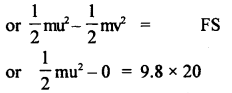
Question 43
A stone of mass 5 kg falls from the top of a cliff 30 m high and buries itself one meter deep into the sand. Find the average resistance offered and time taken to penetrate into the sand.
Answer:
Here, m = 5 kg
h = 30 m
S = 1 m
P.E. of stone = mgh = 5 × 9.8 × 30 = 1470 J
Let F = average force of resistance offered by the sand and F’ = net upward force.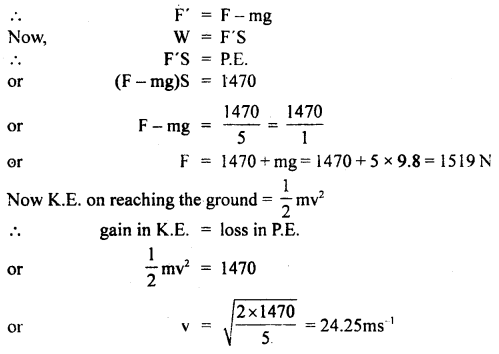
Now momentum of stone before penetration
mu = mv = 5 × 24.25 (∵ here u = v)
Final momentum of stone when it becomes stationary (i.e. v’ = 0)
= mv’ = m(0) = 0
∴ Ft = – mv’ + mu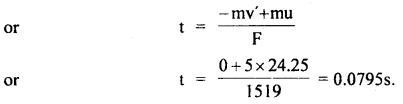
Question 44.
A pump-set is used to lift water to a reservoir of 6000 liters capacity over an average height of 20m. If it takes 1 hour to All the reservoir completely, calculate the work done and the power supplied to the set if its efficiency is 60%, g = 9.8 ms-2.
Answer:
Mass of 1 litre of water = 1 kg .
∴ m = 6000 kg
h = 20 m
∴ W = work done = P.E. = mgh
= 6000 × 9.8 × 20= 11.76 × 10s J
t = 1 h = 3600 s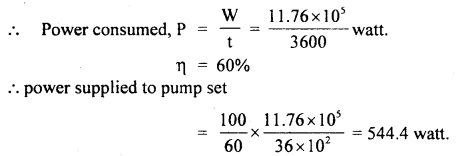
Question 45.
A wooden ball is dropped from a height of 2 m. What is the height up to which the ball will rebound if the coefficient of restitution is 0.5?
Answer:
Here, e =0.5
Let the ball fall from a height h1 from point A and rebound to B at a height of h2.
∴ h1 = 2 m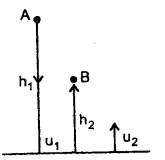
∴ If u1 be the velocity on reaching the ground = velocity of approach and u2 = Velocity on leaving the ground = velocity of separation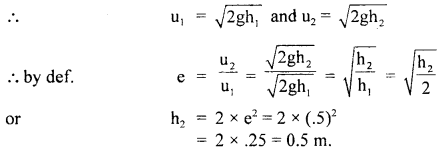
Question 46.
What percentage of K.E. of a moving particle is transferred to the stationary particle of
(a) 9 times it’s mass
Answer:
Let m1 = mass of moving particle = m
and m2 = mass of stationary particle = 9 m
and their velocities are u1 and u2 = 0 (given)
v2 = velocity of the stationary particle after the collision.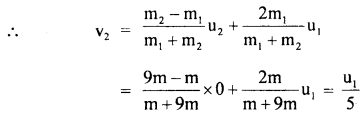
So, % of K.E. transferred to the stationary particle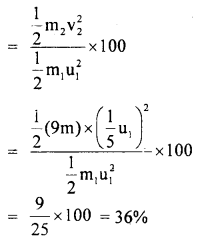
(b) equal mass,
Answer: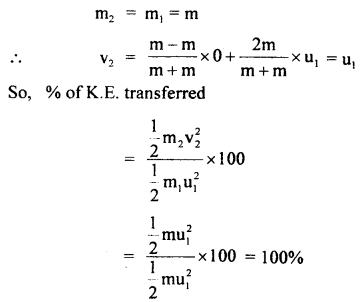
(c)
Answer: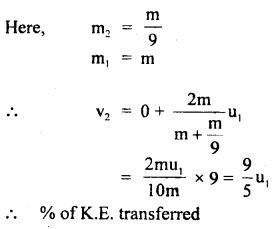
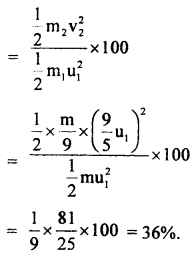
Question 47.
Calculate the work done in raising a stone of mass 6 kg of specific gravity 2 immersed in water from a depth of 4 m to 1 m below the surface of the water. Take g = 10 ms-2.
Answer:
Here, m = 6 kg
∴ weight of stone = 6 × 10 = 60 N
specific gravity of stone = 2
∴ d = density of stone
= 2 × lg cm-3
= 2g cm-3.
∴ volume of stone =
= 3000 × 10-6 m3
= 3 × 10-3 m3
= volume of displaced water.
Weight of water displaced or upward thrust on the stone
= volume × density of water × g
= 3 × 10-3 × 1000 × 10 = 30 N
∴ The net force acting on the stone = weight of stone – upward thrust on the stone
or F = 60 – 30 = 30 N
Distance through which stone is raised = (4 – 1 )m = 3m
∴ work done, W = FS = 30 × 3 = 90 J.
Question 48.
An antenna radiates energy for 24 hours at the rate of 1 kW. Calculate the equivalent mass for radiated energy.
Answer: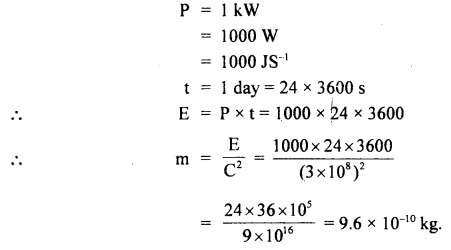
Question 49.
A particle moves from position r1 = 3î + 2ĵ – 6k̂ to position r2 = 14î + 13ĵ – 9k̂ under the action of a force (4î + ĵ + 3k̂)N. Calculate the work done.
Answer:
Here, F = (4î + ĵ + 3k̂)N
Displacement of the particle,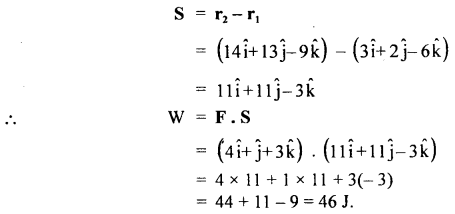
Question 50.
The displacement x of a particle moving in one dimension under the action of a constant force is related to the time by the equation t =
where x is in meters and t is in seconds.
Find (i) the displacement of the particle when its velocity is zero and
(ii) work is done by force in the first six seconds.
Answer: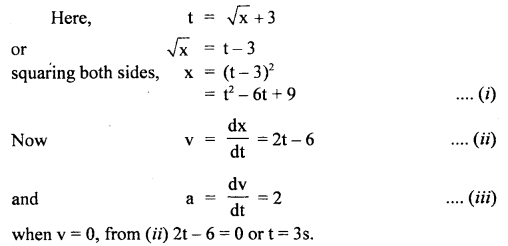
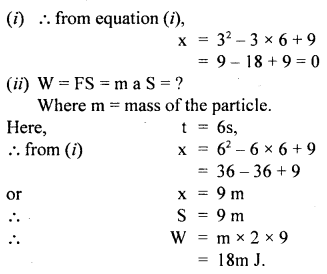





No comments:
Post a Comment
Your Comments help us a lot